Solve for the Exact Same Eigenvalues Again Using an Optimization Approach
Abstract
The newspaper proposes a multi-domain approach to the optimization of the dynamic response of an underactuated vibrating linear organisation through eigenstructure consignment, by exploiting the concurrent design of the mechanical backdrop, the regulator and state observers. The approach relies on handling simultaneously mechanical blueprint and controller synthesis in order to enlarge the set of the achievable performances. The underlying novel idea is that structural properties of controlled mechanical systems should be designed considering the presence of the controller through a concurrent arroyo: this can considerably amend the optimization possibilities. The method is, starting time, developed theoretically. Starting from the definition of the set of feasible organisation responses, divers through the feasible mode shapes, an original formulation of the optimality criterion is proposed to properly shape the allowable subspace through the optimal modification of the design variables. A proper pick of the modifications of the elastic and inertial parameters, indeed, changes the space of the commanded eigenvectors that tin can be achieved through active control and allows obtaining the desired performances. The problem is then solved through a rank-minimization with constraints on the design variables: a convex optimization problem is formulated through the "semidefinite embedding lemma" and the "trace heuristics". Finally, experimental validation is provided through the consignment of a mode shape and of the related eigenfrequency to a cantilever beam controlled past a piezoelectric actuator, in lodge to obtain a region of the beam with negligible oscillations and the other one with large oscillations. The results prove the effectiveness of the proposed approach that outperforms agile control and mechanical design when used alone.
Introduction
Performance optimization through concurrent mechanical and control pattern
Dynamic structural optimization in mechanisms and structures, oftentimes denoted as dynamic response topology optimization, aims at finding the optimal mass and stiffness distribution for obtaining the desired dynamic performances, by optimizing a cost function while satisfying constraints on the feasible parameters. The crux is defining such a cost function, or functioning alphabetize, that properly represents the concrete trouble and its human relationship with the desired performances and should be easily solvable (Yan and Wang 2020). Other features, such as convexity to ensure that global optimal solutions can be constitute regardless of the initial guess (Belotti et al. 2016), are also valuable to ensure meaningful results and bodily optimal results. A reliable definition of the cost function imposes because the presence of the controller too, whenever the structure operates with closed-loop controllers. Indeed, the ever-growing integration between mechanical systems and active devices, such as actuators, imposes a new multidisciplinary and control-oriented blueprint arroyo. Design choices must handle the tight interactions between the mechanical blueprint (e.g. the mass and stiffness properties) and the synthesis of its controller, which likewise comprises the definition of the actuated and sensed variables and the evolution of country observers. In practice, choices should be made with respect to the mechanical parameters needed to achieve the desired performances of the controlled system and the cost role adopted in the optimization should therefore represent this relation. The use of sequential, or even worse, decoupled design approaches that separately consider the mechanical and the command domains, does not tackle effectively these critical interactions and imposes trial-and-error iterations that might converge to less effective solutions. The recent literature on design of actuated mechanical systems has, in contrast, highlighted the need for concurrent and multi-domain approaches (Hehenberger et al. 2013), since the noesis of the controller limits and achievable performances allows for optimizing mechanical constructions and obtaining cost effective solutions. The idea of concurrent blueprint exploiting both active and passive design variables has been recently proved to exist very effective in other field of multi-objective optimization for engineering, such every bit in building engineering (Lee 2019) and control of audio radiation (Zhai et al. 2017). At that place is, withal, notwithstanding a lack of methods to exist used in control-oriented design of underactuated mechanical systems, especially when flexible components are employed either to exploit their resonance features (e.thousand. resonators) or to reduce the overall mass, at the expense of a stiffness reduction.
Most of the approaches proposed so-far are "direct methods" that evaluate different solutions obtained by changing some arrangement parameters. For example, these methods often rely on co-simulation–based integrated optimization methods, which iterate by simulating dissimilar solutions and past predicting the effect of the imposed modifications or the selected controller. An opposite strategy is the one of "inverse" methods whose aim is to compute the modifications necessary to obtain the prescribed dynamic behaviour by solving some mathematical bug, such as inverse eigenvalue bug. The development of inverse, concurrent approaches for the design of actuated mechanical systems requires the explicit definition of the performance targets, e.1000. through some metrics of measurable properties, and of numerical methods for achieving such performances.
Amongst the different approaches, a common and effective approach for defining the desired dynamic properties in vibrating systems is through the shapes, natural frequencies and damping of their vibrational modes, i.e. the eigenstructure. A less investigated field is the assignment of antiresonances (encounter due east.g. Belotti et al. 2020; Richiedei et al. 2019) or antiresonances together with natural frequencies (Richiedei et al. 2020). Natural frequencies and damping, i.e. the eigenvalues of the eigenvalue problem, fix stability and speed of response, while the way shapes, i.e. the eigenvectors, ascertain the spatial shape of the vibration and set up the sensitivities of the corresponding eigenvalues to model parameters. Fifty-fifty though the control theory is usually focused on simply the assignment of eigenvalues, as proved by the several approaches developed in the contempo literature, assigning the eigenvectors too can be more advantageous (Moore 1976). Hence, several approaches accept been proposed to solve the task of eigenstructure assignment (EA), by exploiting either passive modifications of the system parameters (such as masses or stiffnesses) through dynamic structural modification (see east.g. Jihong and Weihong 2006; Hernandes and Suleman 2014; Belotti et al. 2016; Belotti et al. 2018b; Thomas et al. 2020), or active command (meet e.g. Schulz and Inman 1994, Triller and Kammer 1997, Kim et al. 1999, Zhang et al. 2014). The always-growing integration between mechanical systems and agile devices, such as actuators, imposes all the same a more than integrated approach that takes advantage of the features of both active and passive approaches to boost the achievable performances. Hence, design choices must handle the tight interactions between the mechanical design of a system and the synthesis of its controller, which besides comprises the development of state observers (Caracciolo et al. 2008).
In the light of this demand, the employ of "hybrid pattern approaches" (i.eastward. combined active and passive approaches) to eigenstructure assignment is very promising, as information technology has been already proved in other similar applications, such as pole placement in disproportionate systems (Ouyang 2011) or vibration damping through mechanical (Corr and Clark 2002) or piezoelectric dampers (Tang and Wang 2004). The idea of applying hybrid approaches to assign eigenvalues and the related eigenvectors has been originally proposed in Richiedei and Trevisani (2017) and then extended in Belotti and Richiedei (2018) to overcome the limitations of using either passive modifications or active control lonely in the challenging task of EA. On the one mitt, the performances achievable through dynamic structural modification are express past the symmetric nature of the modifications and by the constraints on their viable values. On the other manus, the gear up of eigenvectors that can be achieved through state-feedback active control is severely restricted: organization controllability does not allow assigning any capricious eigenvector, unless the system is fully actuated. Indeed, all the achievable eigenvectors lie in a subspace which depends on the "mechanical properties" of the arrangement (i.e. stiffness, mass and damping matrices) and of the topology of the actuation system (Moore 1976). Hence, EA is very challenging for underactuated systems, and peculiarly in the presence of rank-one control (i.e. in the presence of just one independent control strength). As previously mentioned, hybrid command allows achieving better results in EA: the modification of inertial and elastic parameters is exploited to alter the allowable subspace in such a way that the desired eigenpairs can be assigned through closed-loop control.
Objectives and contributions of the newspaper
By taking advantage of the theoretical formulation introduced past Belotti and Richiedei (2018), this paper proposes an integrated approach to EA for a cantilever beam controlled through a piezoelectric actuator and validates information technology experimentally. Beams are widely used as structural elements in many technology issues, and the optimal design of these systems is still investigated in the very recent literature in the field of structural optimization, such as for example in Aydin et al. (2020) or Hauser and Wang (2018). A dissimilar goal is investigated in this paper, and a new design method is proposed through a concurrent and multi-domain arroyo. The target of the blueprint assumed in this work to bear witness the need of a concurrent optimization approach is to alter both the shape and the frequency of a vibrational style of the beam to reduce vibrations near the clamped cease, while magnifying the oscillations near the free stop. This is an example of vibration confinement, i.e. shaping vibrations and so that they have much smaller amplitude in concerned area than in the remaining role of the construction, which is an application where EA is very attractive (meet e.k. Tang and Wang 2004; Andry et al. 1983). Such a beam optimization might be useful, for case, for designing compliant mechanisms which often are based on cantilever beams. Despite its apparent simplicity, such a job is difficult to solve if passive control or active command are used alone. Indeed, the presence of rank-i control in a multi-dimensional arrangement does not permit the control specifications to be achieved. The analysis of this limitation through the definition of an "allowable subspace" leads to the formulation of a new optimality benchmark for the structural optimization. The problem is and then solved as a rank-minimization with constraints on the design variables. A benefit of this formulation is that a convex problem is obtained, and there is no need to perform repetitious solution of the generalized eigen-problem, which is commonly recognized every bit a cumbersome calculation in topology optimizations (see eastward.g. the discussion provided in Zheng et al. 2017).
The application of the method to a existent device introduces another critical issue: since no direct measurement of the whole state vector is possible, a state observer must exist implemented for the real-time estimation of the state to be fed back. The control and ascertainment spillover (Caracciolo et al. 2008) and the perturbation of the mode shapes due to the utilize of reduced-order observers are therefore handled in the newspaper, and an arroyo to evaluate their affect is proposed. Hence, the observer synthesis can exist likewise included in this improved integrated approach, since the separation principle between controller and observer does not concord anymore in cases similar the one discussed here. Some preliminary results of this research take been presented in the conference newspaper (Belotti et al. 2017). Here, both an improved theory and a new experimental campaign are proposed, to include the observer synthesis within the blueprint process in a more integrated manner and hence extend the idea of concurrent and multidisciplinary design to the observer synthesis. A more constructive approach for the numerical optimization through the rank-minimization is exploited besides.
The paper develops the theory with reference to the mentioned cantilever beam controlled through a piezoelectric actuator: the models (Section 2), the EA method (Sections 3 and four) and the issues related to the observer (Section 5) volition exist discussed with reference to such a arrangement, which tin can be assumed as a meaningful example and for which detailed experimental results are reported in Department half dozen. However, all the methods and models can be extended and applied to other underactuated vibrating systems, with an arbitrary number of control forces and in the presence of damping too.
Organisation model
Model of the axle
Let usa assume that the cantilever beam is modelled through a suitable number of finite elements, such as beam elements, leading to a model with N degrees of freedom (DOFs), collected in vector q . The finite element model of the beam is represented by the beam mass (M ∈ℝ Northward ×N ), stiffness (K ∈ℝ N ×Due north ) and damping (C ∈ℝ Northward ×Due north ) matrices, where f C (t) is the vector of the external control forces (or torques), B the distribution matrix of the command forces, f D (t) the vector of the external disturbance forces (or torques) and B D the distribution matrix of the disturbance forces. Finally, t is the fourth dimension. Hence, the system is represented through the post-obit linear, time-invariant model:
$$ \mathbf{Yard}\ddot{\boldsymbol{q}}(t)+\mathbf{C}\dot{\boldsymbol{q}}(t)+\mathbf{K}\boldsymbol{q}(t)=\mathbf{B}{\boldsymbol{f}}_C(t)+{\mathbf{B}}_D{\boldsymbol{f}}_D(t) $$
(i)
Two obvious assumptions are made on B: it is a full rank matrix, with Due north B being its rank, and it ensures that the organisation is fully controllable, i.due east. rank([M λ i two +C λ i +G B]) =N for whatever open-loop eigenfrequencies λ i . The latter requirements ensure that any fix of desired eigenfrequencies can be obtained, and it is a necessary (but not sufficient) requirement in the case of agile command. Additionally, since underactuated systems are discussed here, N B <N.
In the instance of lightly damped systems, it is a common practice in the literature to correspond the system through an undamped model and then to formulate the structural modification trouble with real eigenvectors and eigenvalues. This assumption, which is assumed in the following of the newspaper, drastically simplifies the design trouble and improves its numerical conditioning since real functions are obtained. Nonetheless, the theory proposed tin can be extended to dissipative systems where damping cannot be neglected, as shown in Belotti and Richiedei (2018).
Model of the piezoelectric actuator
The control forcefulness f C (t) is assumed to be exerted past one or more piezoelectric actuators, which are here modelled through linear theory proposed by Gaudenzi et al. (2000). Nonlinearities, such as hysteresis or gain variability, are neither modelled nor deemed for, and hence are just regarded as uncertainties that crusade minor deviations from the theoretical results.
The force distribution vector for each actuated finite chemical element (denoted B actuated), which is assumed to be actuated by just one actuator, is computed past integrating the shape function of the Euler-Bernoulli beam over the length l of the finite element, which equals the length of the piezoelectric patch:
$$ {\mathbf{B}}_{\mathrm{actuated}}={\int}_0^l{\left\{-\frac{6}{l^two}+\frac{12s}{fifty^iii}\kern0.5em -\frac{iv}{50}+\frac{6s}{50^two}\kern0.5em \frac{6}{fifty^2}-\frac{12s}{fifty^3}\kern0.5em -\frac{2}{fifty}+\frac{6s}{l^ii}\correct\}}^T ds $$
(2)
The remaining entries of B are zero.
By integrating (two), each actuator is modelled as ii contrary torques of magnitude F C applied at both ends of the piezoelectric patch, as represented in Fig. one. These torques are, in plough, modelled as proportional to the practical voltage (Preumont 2011), with a gain whose value can be identified through experimental assay or through data provided by the patch manufacturer.
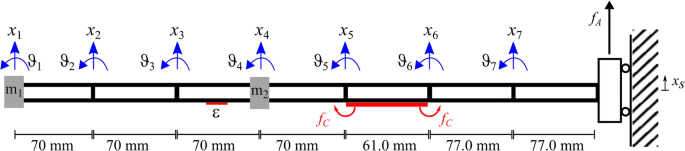
Model of the experimental setup (cantilever beam and sideslip-table)
Finally, the inertial and elastic contributions of the actuator have been too represented through additive mass and stiffness matrices Gaudenzi et al. (2000) based on the Euler-Bernoulli linear theory, named G PZ and G PZ , respectively:
$$ {\displaystyle \begin{array}{c}{\mathbf{M}}_{PZ}=\frac{m_{pz}}{420}\left[\begin{assortment}{ccc}156& 22l& 54\kern0.5em -13l\\ {}22l& iv{l}^ii& 13l\kern0.5em -iii{l}^2\\ {}\brainstorm{array}{c}54\\ {}-13l\stop{array}& \begin{assortment}{c}13l\\ {}-3{fifty}^2\end{array}& \begin{array}{cc}\begin{array}{c}156\\ {}-22l\cease{array}& \begin{assortment}{c}-22l\\ {}4{l}^ii\end{array}\end{array}\end{array}\right]\\ {}{\mathbf{Yard}}_{PZ}={E}_{pz}\frac{h_{eq}^3}{3}\left[\begin{assortment}{ccc}12/{l}^3& six/{l}^ii& \begin{assortment}{cc}-12/{l}^iii& half-dozen/{l}^2\end{assortment}\\ {}vi/{l}^2& four/50& \begin{array}{cc}-six/{fifty}^2& ii/50\end{array}\\ {}\brainstorm{array}{c}-12/{50}^3\\ {}six/{l}^ii\end{array}& \begin{array}{c}-6/l\\ {}two/l\end{array}& \brainstorm{array}{cc}\begin{array}{c}12/{l}^three\\ {}-6/{l}^2\stop{assortment}& \begin{assortment}{c}-6/{l}^2\\ {}4/fifty\end{assortment}\end{array}\end{array}\right]\finish{array}} $$
(3)
The post-obit properties of the piezoelectric patch have been introduced: m pz is the overall mass, E pz is the Immature modulus, h pz is the thickness, and h eq has been defined every bit follows:
$$ {h_{eq}}^3={h_{pz}}^iii+iii{\delta}^ii{h}_{pz}-3\delta {h}_b{h}_{pz}-3\delta {h_{pz}}^2+\frac{3}{4}{h_b}^2{h}_{pz}+\frac{3}{ii}{h}_b{h_{pz}}^two $$
(four)
In (iv), δ denotes the perturbation of the neutral axis due to the presence of the actuator bonded to the beam, compared with the one of the beam without piezoelectric patch.
Manner shape assignment through state-feedback control
The aim of EA through country-feedback control is to calculate the gain matrices F and G leading to the desired eigenpairs, henceforth denoted every bit \( {\left(\overset{\sim }{\lambda },\overset{\sim }{\boldsymbol{u}}\right)}_i \):
$$ {\boldsymbol{f}}_C(t)=-\left({\mathbf{F}}^{\mathrm{T}}\dot{\boldsymbol{q}}(t)+{\mathbf{Thou}}^{\mathrm{T}}\boldsymbol{q}(t)\right) $$
(v)
State-feedback, as well as sometimes land derivative feedback (see e.g. Araújo et al. 2016), are widely adopted in assigning the organisation poles whenever the system is controllable. The controllability assumption is, in contrast, not sufficient for EA, since the necessary status for obtaining an arbitrary mode shape is more restrictive. Indeed, the pair \( {\left(\overset{\sim }{\lambda },\overset{\sim }{\boldsymbol{u}}\right)}_i \) is an eigenpair of the controlled arrangement if and only if it satisfies the following eigenvalue trouble:
$$ \left[\mathbf{Grand}{{\overset{\sim }{\lambda}}_i}^two+\mathbf{C}{\overset{\sim }{\lambda}}_i+\mathbf{K}\right]{\overset{\sim }{\boldsymbol{u}}}_i+\mathbf{B}\left[{\overset{\sim }{\lambda}}_i{\mathbf{F}}^T+{\mathbf{G}}^T\right]{\overset{\sim }{\boldsymbol{u}}}_i=\mathbf{0} $$
(6)
Past defining vector \( {\boldsymbol{\phi}}_i=\left[{\overset{\sim }{\lambda}}_i{\mathbf{F}}^T+{\mathbf{G}}^T\right]{\overset{\sim }{\boldsymbol{u}}}_i \), (6) is equivalent to the following condition:
$$ \left[\mathbf{Grand}{{\overset{\sim }{\lambda}}_i}^2+\mathbf{C}{\overset{\sim }{\lambda}}_i+\mathbf{K}\kern0.5em \mathbf{B}\right]\left[\begin{assortment}{c}{\overset{\sim }{\boldsymbol{u}}}_i\\ {}{\boldsymbol{\phi}}_i\cease{assortment}\right]=\mathbf{0} $$
(7)
\( {\boldsymbol{\phi}}_i\in {\mathbb{C}}^{N_b} \) is an capricious vector, since the gain matrices are arbitrary. Hence \( {\overset{\sim }{\boldsymbol{u}}}_i \) is an assignable eigenvector if and only if \( \left[\begin{array}{c}{\overset{\sim }{\boldsymbol{u}}}_i\\ {}{\boldsymbol{\phi}}_i\end{array}\right] \) belongs to the zip-infinite (represented through the operator \( \mathcal{North} \)) of \( \left[\mathbf{M}{{\overset{\sim }{\lambda}}_i}^2+\mathbf{C}{\overset{\sim }{\lambda}}_i+\mathbf{K}\kern0.75em \mathbf{B}\right] \):
$$ \left[\begin{array}{c}{\overset{\sim }{\boldsymbol{u}}}_i\\ {}{\boldsymbol{\phi}}_i\end{array}\right]\in \mathcal{Northward}\left(\left[\mathbf{Chiliad}{{\overset{\sim }{\lambda}}_i}^two+\mathbf{C}{\overset{\sim }{\lambda}}_i+\mathbf{One thousand}\kern0.5em \mathbf{B}\right]\correct) $$
(8)
The space \( \Psi \left({\overset{\sim }{\lambda}}_i\right)=\mathcal{Northward}\left(\left[\mathbf{Thousand}{{\overset{\sim }{\lambda}}_i}^2+\mathbf{C}{\overset{\sim }{\lambda}}_i+\mathbf{K}\kern0.5em \mathbf{B}\correct]\right) \) is named the allowable subspace and spans all the eigenvectors, associated to \( {\overset{\sim }{\lambda}}_i \), that can be achieved through active control for the system nether investigation.
If the organization is controllable, then \( \dim \Psi \left({\overset{\sim }{\lambda}}_i\correct)=\operatorname{rank}\left(\mathbf{B}\right) \). Hence, the number of arbitrary terms of the eigenvectors is equal to the number of independent control forces. Hence, any arbitrary eigenvector cannot exist usually obtained through active control in the case of underactuated systems (i.e. rank(B) <N). In dissimilarity, any arbitrary eigenvector tin be obtained in the example of fully-actuated organization (i.e. rank(B) =N). Equation (8) clearly corroborates that the achievable performances of the controlled system are constrained by the features of the mechanical construction, equally stated in Section i. Hence, this limitation should exist accounted in the stages of the mechanical pattern.
Dynamic structural modification oriented to state-feedback control
In the following developments, velocity feedback and damping matrix are non considered, to represent the instance in which information technology is not desired to damp a lightly-damped arrangement. Hence, real eigenvectors and eigenvalues are adopted. However, the theory can exist also extended in the case of damped systems, as shown by Belotti and Richiedei (2018).
Permit u.s.a. assign a set of N e eigenpairs \( {\left(\overset{\sim }{\lambda },\overset{\sim }{\boldsymbol{u}}\right)}_i \). Hybrid control consists in modifying the allowable subspace \( \Psi \left({\overset{\sim }{\lambda}}_i\right) \) through ΔM and ΔK to obtain a new subspace \( \hat{\Psi}\left({\overset{\sim }{\lambda}}_i\right) \) to which the desired eigenvector belongs:
$$ \left[\begin{array}{c}{\overset{\sim }{\boldsymbol{u}}}_i\\ {}{\boldsymbol{\phi}}_i\end{assortment}\right]\in \mathcal{N}\left(\left[\left(\mathbf{Grand}+\Delta \mathbf{Grand}\right){{\overset{\sim }{\lambda}}_i}^2+\left(\mathbf{M}+\Delta \mathbf{K}\right)\kern0.75em \mathbf{B}\correct]\right)=\hat{\Psi}\left({\overset{\sim }{\lambda}}_i\right) $$
(9)
for some arbitrary \( {\boldsymbol{\phi}}_i\in {\mathbb{C}}^{N_b} \).
The calculation of ΔM and ΔK satisfying (9) can exist solved as a rank-minimization trouble. This formulation is advantageous since several constructive numerical algorithms problems have been recently developed. Additionally, it is not necessary to compute the allowable subspace.
In order to prefer the rank-minimization formulation, the eigenvalue problem of the modified system is written as the following linear arrangement:
$$ \mathbf{B}{\boldsymbol{\phi}}_i=\left[\left(\mathbf{Yard}+\Delta \mathbf{M}\correct){{\overset{\sim }{\lambda}}_i}^2+\left(\mathbf{K}+\Delta \mathbf{K}\correct)\right]{\overset{\sim }{\boldsymbol{u}}}_i $$
(10)
that can be expressed in the following grade, with the obvious significant of d i :
$$ \mathbf{B}{\boldsymbol{\phi}}_i={\boldsymbol{d}}_i $$
(eleven)
Equation (11) has a solution if and only if the following condition holds:
$$ \operatorname{rank}\left(\left[\mathbf{B}|{\boldsymbol{d}}_i\right]\right)=\operatorname{rank}\left(\mathbf{B}\right) $$
(12)
By introducing matrix \( \mathbf{D}=\left[{\boldsymbol{d}}_1|\dots |{\boldsymbol{d}}_{N_e}\right]\in {\mathbb{R}}^{N\times {North}_e} \), the system in (11) can be solved for any i = 1, …, N e if and only if:
$$ \operatorname{rank}\left(\left[\mathbf{B}|\mathbf{D}\right]\right)={N}_B. $$
(13)
Since rank([B|D]) = rank(B) + rank([I −BB +]D), such a rank status, in turn, holds if and only if
$$ \operatorname{rank}\left(\left[\mathbf{I}-\mathbf{B}{\mathbf{B}}^{+}\right]\mathbf{D}\right)=0. $$
(xiv)
where B + is the pseudoinverse of matrix B. The unique exact solution of (14) is [I −BB +]D = 0. However, given the presence of several requirements on the desired eigenvectors, which are not ensured to be achievable specially when highly underactuated systems are handled, an approximate solution of (14) should be sought. The difficulties in achieving an exact solution are exacerbated by the presence of constraints on the topologies of ΔM and ΔK and on the commanded organisation modifications, due to constraints. Hence, it is proposed to transform the verbal problem to an optimization-based formulation aimed at finding ΔM and ΔK that solve the following rank-minimization problem:
$$ {\displaystyle \begin{array}{cc}\operatorname{minimize}& \operatorname{rank}\left(\left[\mathbf{I}-\mathbf{B}{\mathbf{B}}^{+}\correct]\mathbf{D}\right)\\ {}\mathrm{subject}\ \mathrm{to}& \left(\boldsymbol{\Delta} \mathbf{M},\boldsymbol{\Delta} \mathbf{K}\right)\in \Gamma \end{array}} $$
(15)
Γ is the set of the allowable modifications of the mass and stiffness parameters in ΔM and ΔK. In this fashion, the being of a solution that optimally approximates the desired eigenvectors is assured for any not-empty Γ. The modification problem of the allowable subspaces can therefore be thought every bit finding the modification matrices, such that (15) holds.
The solution of the rank-minimization trouble (15) can be performed through some heuristic algorithms for rank-minimization. In particular, the semidefinite embedding lemma proposed by Fazel et al. (2003) can be adopted to solve the problem, by taking advantage of the so-called trace heuristics which replaces the rank with the trace, as frequently done in solving several optimization problem (see e.g. Fazel et al. (2001)). This formulation leads to a convex minimization problem. Following such a theoretical issue, trouble in (15) is further recast equally follows:
$$ {\displaystyle \brainstorm{array}{cc}\operatorname{minimize}& \mathrm{trace}\kern0.33em \left(\operatorname{diag}\left(\mathbf{Y},\mathbf{Z}\right)\correct)\\ {}\mathrm{subject}\ \mathrm{to}& \left\{\begin{array}{c}\left[\begin{assortment}{cc}\mathbf{Y}& \left[\mathbf{I}-\mathbf{B}{\mathbf{B}}^{+}\correct]\mathbf{D}\\ {}{\mathbf{D}}^T{\left[\mathbf{I}-\mathbf{B}{\mathbf{B}}^{+}\right]}^T& \mathbf{Z}\end{array}\correct]\succcurlyeq 0\\ {}\left(\boldsymbol{\Delta} \mathbf{Grand},\boldsymbol{\Delta} \mathbf{K}\right)\in \Gamma .\end{assortment}\right.\end{assortment}} $$
(16)
for ii arbitrary symmetric matrices Y ∈ℝ 1000 ×k and Z ∈ℝ n ×due north . The inequality ≽0 denotes that the matrix on the left-paw side should be positive semidefinite. The optimization problem obtained is convex if the feasibility constraint set Γ is chosen every bit a convex set. This is a very important feature of the proposed problem.
Once the modifications matrices have been computed past solving numerically the rank-minimization problem in (sixteen), the gains of the controller should be calculated through one of the several methods for eigenstructure assignment. If the desired eigenvector \( {\overset{\sim }{\boldsymbol{u}}}_i \) does not belong to the allowable subspace of the modified system, it should be replaced with its orthogonal projection onto the allowable subspace of the modified system (Richiedei and Trevisani 2017–Andry et al. 1983), named \( {\overset{\sim }{\boldsymbol{u}}}_{ip} \):
$$ {\overset{\sim }{\boldsymbol{u}}}_{ip}={\boldsymbol{\Psi}}_i{\left({\boldsymbol{\Psi}}_i^T{\boldsymbol{\Psi}}_i\right)}^{-i}{\boldsymbol{\Psi}}_i^T{\overset{\sim }{\boldsymbol{u}}}_i $$
(17)
Ψ i (for any alphabetize i) is a matrix whose columns span the commanded subspace of the modified system. \( {\overset{\sim }{\boldsymbol{u}}}_{ip} \) is the allowable eigenvector that provides the tightest approximation of the desired i \( {\overset{\sim }{\boldsymbol{u}}}_i \), whenever \( {\overset{\sim }{\boldsymbol{u}}}_i \) is unfeasible. The project of the desired eigenvector onto the allowable subspace of the modified system provides a better approximation than the projection onto the allowable subspace of the original organization, thanks to the clever synthesis of ΔM and ΔK.
Introduction of a state-observer
In the implementation of state-feedback control, it is a mutual need to replace the measured, actual state (\( \dot{\boldsymbol{q}} \) and q ) with the estimated one (Caracciolo et al. 2008). Indeed, measurement of all the country variables in structures or in multibody systems is usually very hard (Palomba et al. 2017; Sanjurjo et al. 2018). Estimation is provided past a country observer (or state estimator), which reconstructs missing country variables by merging the model, expressed every bit a kickoff-order country-space model, and a meaningful set of measurements with a prediction-correction logic (Palomba et al. 2017). In the light of a concurrent design, the effect of the state observer should exist included in the overall arroyo too, and the limitations due to the computational endeavor required for existent time estimation should be investigated.
To develop a state observer, a first-order formulation of the organisation model in (1) is needed, by writing it in the following grade:
$$ \left\{\begin{array}{c}\ddot{\boldsymbol{q}}(t)\\ {}\dot{\boldsymbol{q}}(t)\end{assortment}\right\}=\left[\begin{assortment}{cc}-{\mathbf{M}}^{-1}\mathbf{C}& -{\mathbf{Grand}}^{-one}\mathbf{Thou}\\ {}\mathbf{I}& \mathbf{0}\stop{assortment}\right]\left\{\brainstorm{assortment}{c}\dot{\boldsymbol{q}}(t)\\ {}\boldsymbol{q}(t)\end{array}\right\}+\left\{\begin{array}{c}{\mathbf{M}}^{-one}\mathbf{B}\\ {}\mathbf{0}\cease{array}\right\}{\boldsymbol{f}}_C(t)+\left\{\begin{assortment}{c}{\mathbf{K}}^{-1}{\mathbf{B}}_D\\ {}\mathbf{0}\cease{assortment}\right\}{\boldsymbol{f}}_D(t) $$
(18)
The state-infinite model in (xviii) can be written in the more compact class of (19), with the obvious definition of matrices A χ , B Cχ , B Dχ and C χ and of the state vector \( \boldsymbol{\upchi} =\left\{\begin{assortment}{c}\overset{\cdot }{\boldsymbol{q}}\\ {}\boldsymbol{q}\end{assortment}\right\} \):
$$ \left\{\begin{array}{fifty}\dot{\boldsymbol{\upchi}}(t)={\mathbf{A}}_{\chi}\boldsymbol{\upchi} (t)+{\mathbf{B}}_{C\chi}{\boldsymbol{f}}_C(t)+{\mathbf{B}}_{D\chi}{\boldsymbol{f}}_D(t)\\ {}\mathbf{y}(t)={\mathbf{C}}_{\chi}\boldsymbol{\upchi} (t)\end{assortment}\right. $$
(19)
An effective approach to the synthesis of land observers for linear vibrating systems is the use of a linear Luenberger observer, such as the Kalman filter, based on a reduced-order model on a modal base. Such a option is motivated by the need of reducing the computational effort for the real-time solution of the observer differential equations, by reducing the number of the equations, i.e. the size of the model adopted for state estimation. The utilise of reduced model is widely proposed in the literature for simplifying both the model-based pattern (Palomba et al. 2015; Xiao et al. 2020; Delissen et al. 2020) and the command synthesis (Caracciolo et al. 2008). The model in (19) is therefore recast in the modal canonical form by using the linear transformation
$$ \mathbf{z}(t)=\mathbf{T}\boldsymbol{\upchi } (t), $$
(twenty)
where vector z denotes the modal coordinates of the outset-gild model and T ∈ℝ twoN × iiN is the transformation matrix, leading to the following linear system:
$$ \left\{\begin{assortment}{l}\dot{\mathbf{z}}\ (t)={\mathbf{A}}_Z\mathbf{z}(t)+{\mathbf{B}}_{CZ}{\boldsymbol{f}}_C(t)+{\mathbf{B}}_{DZ}{\boldsymbol{f}}_D(t)\\ {}\mathbf{y}\ (t)={\mathbf{C}}_Z\mathbf{z}(t)\end{array}\correct. $$
(21)
The new model matrices are obtained equally follows: A Z =TA χ T −1, B CZ =TB Cχ , B DZ =TB Dχ and C Z =C χ T −1.
Reduction consists in partitioning the modal base z into a fix of less relevant modes z N , that are ordinarily the highest frequency ones, and a set of dominant ones z R , that are normally the lowest frequency ones or those with the greatest contribution to the system response (Palomba et al. 2015):
$$ \left\{\begin{array}{l}\left\{\begin{array}{c}{\dot{\mathbf{z}}}_{\mathrm{R}}(t)\\ {}{\dot{\mathbf{z}}}_{\mathrm{Northward}}(t)\end{array}\right\}=\left[\begin{array}{cc}{\mathbf{A}}_R& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{A}}_N\finish{array}\right]\left\{\begin{array}{c}{\mathbf{z}}_{\mathrm{R}}(t)\\ {}{\mathbf{z}}_{\mathrm{North}}(t)\end{array}\right\}+\left\{\begin{array}{c}{\mathbf{B}}_{CR}\\ {}{\mathbf{B}}_{CN}\terminate{array}\right\}{\boldsymbol{f}}_C(t)+\left\{\begin{array}{c}{\mathbf{B}}_{DR}\\ {}{\mathbf{B}}_{DN}\end{assortment}\right\}{\boldsymbol{f}}_D(t)\\ {}\mathbf{y}(t)=\left[{\mathbf{C}}_R\kern0.5em {\mathbf{C}}_N\right]\left\{\brainstorm{array}{c}{\mathbf{z}}_{\mathrm{R}}(t)\\ {}{\mathbf{z}}_{\mathrm{Due north}}(t)\terminate{array}\right\}\stop{array}\right. $$
(22)
The matrices in (22) are partitions of matrices in (21). The reduced social club model is obtained by discarding z N (the so-chosen "neglected modes") and hence past just considering the subsystem fabricated by states z R (the so-chosen "retained modes"):
$$ \left\{\begin{array}{l}{\dot{\mathbf{z}}}_{\mathrm{R}}(t)={\mathbf{A}}_R{\mathbf{z}}_{\mathrm{R}}(t)+{\mathbf{B}}_{CR}{\boldsymbol{f}}_C(t)+{\mathbf{B}}_{DR}{\boldsymbol{f}}_D(t)\\ {}\mathbf{y}(t)\simeq {\mathbf{C}}_R{\mathbf{z}}_{\mathrm{R}}(t)\end{array}\right. $$
(23)
The neglected modes are those with the lowest observability and controllability, that are in exercise weakly excited in the range of frequency of interest. Additionally, the low-pass filtering of the sensor measurements and the actuator bandwidth farther reduce their contribution in the organisation response. Hence, their fourth dimension trajectory tin exist finer approximated every bit equal to zero and they tin be discarded in the land observer (Caracciolo et al. 2008). The touch on of such a choice tin can be evaluated through the relations proposed in Department 5.1.
Starting from the reduced model in (23), the following scheme of continuous-time state observer can exist implemented for estimating z R and hence χ (the lid is adopted to mark the estimated quantities):
$$ \left\{\brainstorm{assortment}{l}{\hat{\dot{\mathbf{z}}}}_{\mathrm{R}}(t)={\mathbf{A}}_R{\hat{\mathbf{z}}}_R(t)+{\mathbf{B}}_{CR}{\boldsymbol{f}}_C(t)+{\mathbf{B}}_{DR}{\boldsymbol{f}}_D(t)+\boldsymbol{50}\left(\mathbf{y}(t)-\chapeau{\mathbf{y}}(t)\right)\\ {}\hat{\mathbf{y}}(t)={\mathbf{C}}_R{\hat{\mathbf{z}}}_R(t)\end{array}\right. $$
(24)
Matrix L is the observer gain, that can exist for instance computed through the Kalman's theory, and aims at optimally trading between the prediction (i.e. \( {\mathbf{A}}_R{\hat{\mathbf{z}}}_R(t)+{\mathbf{B}}_{CR}{\boldsymbol{f}}_C(t)+{\mathbf{B}}_{DR}{\boldsymbol{f}}_D(t) \)) and the correction (i.e. \( \mathbf{y}(t)-\hat{\mathbf{y}}(t) \)).
Finally, the estimated values of the physical coordinates are computed through the changed of the transformation matrix:
$$ \hat{\boldsymbol{\upchi}}(t)={\mathbf{T}}^{-1}\lid{\mathbf{z}}(t)={\mathbf{T}}^{-one}\left\{\begin{array}{c}{\hat{\mathbf{z}}}_{\mathrm{R}}(t)\\ {}{\hat{\mathbf{z}}}_{\mathrm{Northward}}(t)\finish{array}\correct\}={\mathbf{T}}^{-one}\left\{\brainstorm{assortment}{c}{\lid{\mathbf{z}}}_{\mathrm{R}}(t)\\ {}\mathbf{0}\end{array}\right\} $$
(25)
Since the neglected modes are those that do not significantly participate in the system response, they are, in practice, estimated as naught: \( {\hat{\mathbf{z}}}_N(t)=\mathbf{0} \) and \( {\chapeau{\dot{\mathbf{z}}}}_N(t)=\mathbf{0}\forall t \) (Caracciolo et al. 2008). Hence, the following relation is established for the control force, where G R denotes the control gain matrix expressed in the modal base z:
$$ {\boldsymbol{f}}_C(t)=-\left[{\mathbf{F}}^{\mathrm{T}}\kern0.5em {\mathbf{1000}}^{\mathrm{T}}\right]\hat{\boldsymbol{\upchi}}(t)=-\left[\begin{array}{cc}{\mathbf{F}}^{\mathrm{T}}& {\mathbf{M}}^{\mathrm{T}}\cease{array}\right]{\mathbf{T}}^{-1}\left\{\begin{assortment}{c}{\hat{\mathbf{z}}}_R(t)\\ {}{\hat{\mathbf{z}}}_N(t)\end{array}\right\}=-{\mathbf{G}}_R^T{\hat{\mathbf{z}}}_{\mathrm{R}}(t). $$
(26)
Evaluation of the spillover due to the observer
A correct tuning of the observer gain matrix L and a wise choice of the number of retained modes have a crucial part in ensuring the achievement of the desired eigenpair. Indeed, the presence of neglected modes, whose amplitude is not negligible, causes control and observation spillover of the closed-loop system poles and perturbates the associated mode shapes. The touch of model truncation on the overall solution tin can be evaluated through the analysis of the perturbation on the eigenvalues and eigenvectors of interest due to the reduced club observer. These effects tin be evaluated by defining the estimation fault due east(t) on the modes retained in the state observer:
$$ \mathbf{east}(t)={\mathbf{z}}_{\mathrm{R}}(t)-{\hat{\mathbf{z}}}_{\mathrm{R}}(t) $$
(27)
and then by evaluating the eigenstructure of the augmented system. The model of the airtight-loop system, with augmented state to include e(t), is the following one:
$$ \left\{\begin{assortment}{c}{\dot{\mathbf{z}}}_{\mathbf{R}}(t)\\ {}\dot{\mathbf{e}}(t)\\ {}{\dot{\mathbf{z}}}_{\mathbf{N}}(t)\end{array}\correct\}=\left[\begin{array}{ccc}{\mathbf{A}}_R-{\mathbf{B}}_{CR}{\mathbf{G}}_R& {\mathbf{B}}_{CR}{\mathbf{M}}_R& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{A}}_R-\mathbf{L}{\mathbf{C}}_R& \mathbf{L}{\mathbf{C}}_N\\ {}-{\mathbf{B}}_{CN}{\mathbf{One thousand}}_R& {\mathbf{B}}_{CN}{\mathbf{G}}_R& {\mathbf{A}}_N\end{assortment}\correct]\left\{\brainstorm{array}{c}{\mathbf{z}}_{\mathbf{R}}(t)\\ {}\mathbf{due east}(t)\\ {}{\mathbf{z}}_{\mathrm{N}}(t)\end{array}\correct\}+\left\{\begin{array}{c}{\mathbf{B}}_{DR}\\ {}\mathbf{0}\\ {}{\mathbf{B}}_{DN}\end{assortment}\right\}{\boldsymbol{f}}_D(t) $$
(28)
As a kickoff effect, it tin can be noticed that separation principle between the poles of the observer and of the controller system does not concord anymore since the transition matrix in (28) is a not cake triangular matrix because of the control spillover (−B CN Grand R , B CN Yard R ) and observation spillover (LC North ) terms. These terms depend on both the contribution of the residual modes in the organisation response (represented through B CN and C N ) and on the gains of the controller and the observer. Information technology should exist noticed that the separation principle, that is usually formulated with reference to the eigenvalues (Franklin et al. 2015), has a counterpart too for the eigenvectors. If the set of neglected vibrational modes z N is assumed empty, for simplicity, so a block triangular matrix is obtained:
$$ \left[\brainstorm{assortment}{cc}{\mathbf{A}}_R-{\mathbf{B}}_{CR}{\mathbf{Chiliad}}_R& {\mathbf{B}}_{CR}{\mathbf{G}}_R\\ {}\mathbf{0}& {\mathbf{A}}_R-\mathbf{50}{\mathbf{C}}_R\end{array}\right]\left[\begin{array}{cc}{\mathbf{U}}_{contr}& \boldsymbol{\uppsi} \\ {}\mathbf{0}& {\mathbf{U}}_{obs}\end{assortment}\right]=\left[\brainstorm{array}{cc}{\mathbf{U}}_{contr}& \boldsymbol{\uppsi} \\ {}\mathbf{0}& {\mathbf{U}}_{obs}\end{array}\correct]\left[\begin{array}{cc}{\boldsymbol{\Omega}}_{contr}& \mathbf{0}\\ {}\mathbf{0}& {\boldsymbol{\Omega}}_{obs}\finish{array}\right] $$
(29)
Ω contr and U contr are the eigenvalue and eigenvector matrices of the system controlled through state feedback, obtained by solving the eigenvalue trouble for the controlled system alone, unremarkably denoted equally "the command roots" (Franklin et al. 2015):
$$ \left({\mathbf{A}}_R-{\mathbf{B}}_{CR}{\mathbf{G}}_R\right){\mathbf{U}}_{contr}={\boldsymbol{\Omega}}_{contr}{\mathbf{U}}_{contr} $$
(30)
Ω obs and U obs are the eigenvalue and eigenvector matrices of the observer eigenvalue trouble, unremarkably denoted equally "the observer roots" (Franklin et al. 2015):
$$ \left({\mathbf{A}}_R-\mathbf{L}{\mathbf{C}}_R\right){\mathbf{U}}_{obs}={\boldsymbol{\Omega}}_{obs}{\mathbf{U}}_{obs} $$
(31)
Finally, ψ is defined as follows:
$$ \left({\mathbf{A}}_R-{\mathbf{B}}_{CR}{\mathbf{1000}}_R-{\boldsymbol{\Omega}}_{obs}\right)\boldsymbol{\uppsi} =-{\mathbf{B}}_{CR}{\mathbf{K}}_R{\mathbf{U}}_{obs} $$
(32)
The eigenvectors of the "command roots" are \( \left\{\begin{assortment}{c}{\mathbf{U}}_{contr}\\ {}\mathbf{0}\end{array}\correct\} \), despite the presence of the (full-order) observer. Therefore, the observer would non perturbate the mode shape of the vibrational modes under these hypotheses.
The effect of the spillover terms (LC Due north and B CN Grand R ) is to perturbate all the entries of such vectors, whose upper part volition differ from U contr and U obs , and to introduce non-naught entries in the lower part of the eigenvectors of the "command roots". This results in a perturbation of the mode shape of the vibrational modes. Hence, an authentic selection of the retained modes is of primary importance to ensure the accomplishment of the theoretical expectations with negligible perturbation of both the natural frequencies and of the style shapes. This evaluation should be done in accordance with the gain matrices. As far as observation spillover is concerned, it can be reduced also through a conscientious choice of a low-pass filter that partially removes the contribution of the neglected modes in the sensed output, without delaying the measurements in the observer bandwidth. Secondly, sensor placement has also a meaningful contribution in ascertainment spillover because of the presence of matrix C N : skillful locations of the sensors used for the filter correction are those ensuring large displacements for the retained modes and smaller contributions of the neglected ones. As far as control spillover is concerned, the presence of high gains makes the term B N Chiliad R more astringent. Hence, the suitable number of retained modes is also affected by the command gains.
All the above-mentioned statements corroborate that the achievable performances tin can be maximized simply if all the mutual relations between the mechanical system, the controller and the observer are accounted for.
Experimental application
Description of the experimental setup
The experimental application of the hybrid command is proposed through the cantilever beam shown in Fig. 2 whose principal physical parameters are sketched in Fig. 1. The beam is clamped on a sideslip-table actuated by an electrodynamic shaker to provide external base of operations excitation for the identification of the system dynamic model and of the experimental modal analysis. The base excitation behaves as the disturbance force f D of (1). The control force f C is exerted by an off-the-shelf piezoelectric actuator PI DuraAct Patch Transducer (with size 61 × 35 × 0.viii mm, blocking force 775 Northward, and minimum bending radius seventy mm). The actuator patch fits the sixth finite element from the costless cease of the finite chemical element model of the beam, as shown in Fig. ane. Indeed, this position ensures high controllability for the vibrational modes of interest. A PI Due east-413.D2 power amplifier has been used to supply power to the actuator. Off-the-shelf components take been called to demonstrate the ease of implementation of the proposed method, while the optimization of the features of the actuators is out of the scope of this newspaper.

Picture of the experimental setup
The command scheme, which includes the controller and the observer, has been implemented on a PC where a real-fourth dimension kernel interfacing with the operating organization is installed through the MathWorks Real-Time Windows Target.
Every bit for the allowable modifications, it is causeless that just two additional lumped masses can be placed in the 2nd and 7th nodes of the FE model (see Fig. 1), since other nodes are not accessible because of the presence of the actuator and the sensors. These masses are the design variables of the dynamic structural modification whose values should be computed through the method proposed in Department 4. The values of the feasible modifications are constrained by tight lower and upper bounds, i.east. (0, 200 k). Clearly, the larger the constraints, the better the commanded eigenvector is. Notwithstanding, setting tight constraints is common in design practices.
Dynamic model
Eight Euler-Bernoulli beam elements take been adopted to model the clamped beam, leading to 14 DOFs collected in vector q :
$$ \boldsymbol{q}={\left\{{x}_1,{\vartheta}_1,{x}_2,{\vartheta}_2,\dots, {ten}_7,{\vartheta}_7\right\}}^T $$
(33)
The obvious pregnant of the variables introduced in (33) can be inferred from Fig. 1.
The damping matrix C is modelled as a linear combination of M and K, in accordance with the Rayleigh model and has been adopted just for the state observer. In contrast, it has been neglected in the synthesis of both the active control and the parameter modifications.
The model of the complete experimental setup, which also includes the slip-table exploited for the identification of the vibrational mode of interest, requires an additional coordinate, that is the position of the skid-table. Such a coordinate, denoted as x s , tin be notionally idea of as the "rigid-trunk DOF" and defines a moving reference from which small elastic displacements are divers (Belotti et al. 2018a). In Fig. 1, the roller constraints correspond the translation of the sideslip-tabular array adopted for modal analysis and this is the model adopted for the observer too, to account for the external shaker excitation. Since the axle is clamped on the skid-table, the vibrational modes of the cantilever axle with clamped constraint are the aforementioned of those of the beam with roller constraint (except for the one at the nil frequency, that represents the "rigid-body motility" of the roller, which is yet not of interest). Hence, the motility of the whole experimental setup is modelled by the North + ane-dimensional organization of linear differential equations:
$$ \left[\begin{array}{cc}\mathbf{K}& \mathbf{MS}\\ {}{\mathbf{Southward}}^T\mathbf{M}& {\mathbf{S}}^T\mathbf{M}\mathbf{Southward}+{One thousand}_C\end{array}\right]\left\{\brainstorm{array}{c}\ddot{\boldsymbol{q}}\\ {}{\ddot{ten}}_s\end{array}\right\}+\left\{\begin{array}{c}\mathbf{C}\dot{\boldsymbol{q}}\\ {}0\end{array}\right\}+\left\{\begin{array}{c}\mathbf{Grand}\boldsymbol{q}\\ {}0\end{array}\correct\}=\left\{\begin{array}{c}\mathbf{0}\\ {}1\end{array}\right\}{f}_A+\left\{\begin{array}{c}\mathbf{B}\\ {}0\end{array}\right\}{f}_C $$
(34)
S is the vector of the nodal sensitivity coefficients with respect to x due south :
$$ {\left[\mathbf{S}\correct]}_i=\fractional {q}_i/\fractional {x}_s=\left\{\begin{array}{c}\partial {10}_i/\partial {x}_s=one\\ {}\fractional {\vartheta}_i/\fractional {x}_s=0\end{array}\right.\kern1.85em i=i,\dots, N $$
(35)
The scalar variable f A is the force exerted by the actuator that drives the slip-table, whose mass is M C , on the electrodynamic shaker. The scalar variable f C is the nodal torque exerted by the piezoelectric actuator, i.e. the control forcefulness.
Argument of the control specifications
It is wanted to control the beam in such a style that information technology features a vibrational mode at fifty Hz whose shape is pictured in Fig. 3, where information technology is also compared with the closest mode of the original system design (i.eastward. the second ane). Such a value of the desired frequency has been selected as a sample, while the requirement on the fashion shape aims at confining the oscillations of this vibrational style to the parts of the beam about the complimentary end, while isolating the parts of the axle near the clamped end. This is an ambitious target, which tin can be easily achieved with a large number of independent actuators that lead to a multi-dimensional allowable subspace. In contrast, information technology is very difficult to obtain with just 1 actuator since the desired eigenvector does not vest to the commanded subspace of the original organisation. The projection of the desired style shape onto such a subspace approximates the target very roughly, equally shown in Fig. 4: the cosine of the angle betwixt the desired eigenvector and the one obtained is merely 0.524. Thus, it adequately misses the target value 1. This cosine is worse than the one of the uncontrolled (open-loop) original system, whose mode shape ensures a cosine between the desired eigenvector and the bodily one that is 0.867. As for the eigenfrequency, since the system is controllable, the closed-loop pole at 50 Hz tin be obtained exactly, past modifying the original eigenfrequency that is 79.9 Hz.
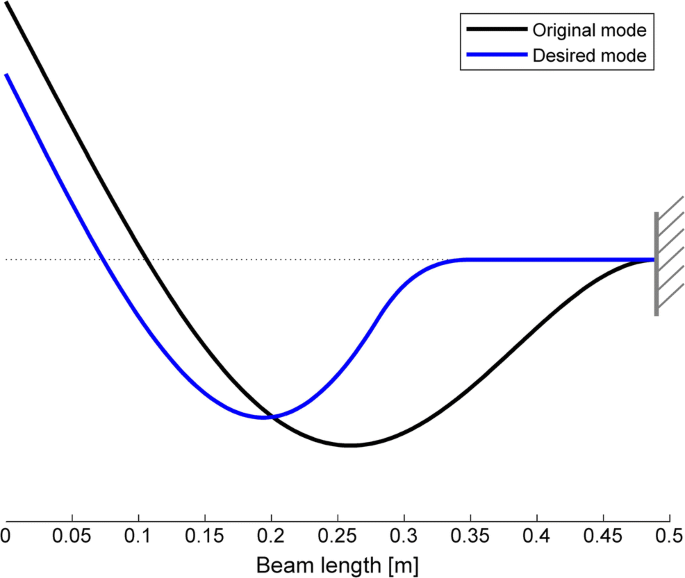
Comparison between the desired mode (50 Hz) and the original one (cosine between the two vectors: 0.867)
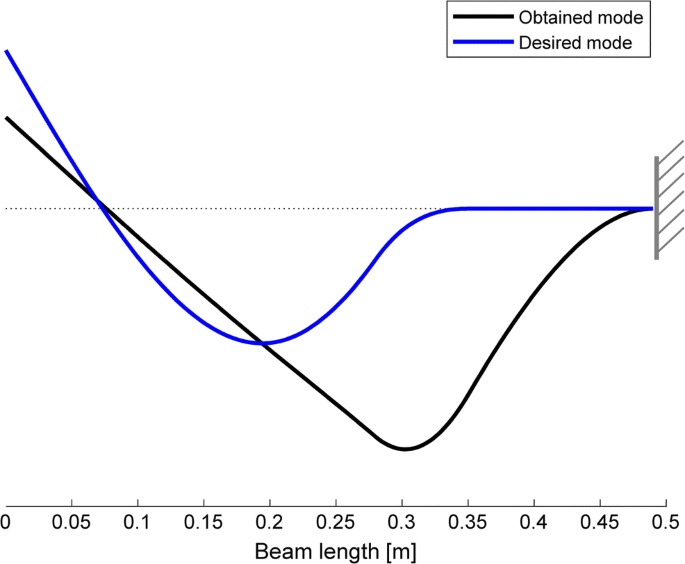
Comparing between the desired mode (50 Hz) and the one obtained with active control (cosine betwixt the ii vectors: 0.524)
If dynamic structural modification is applied solitary, the result obtained is, again, far from existence satisfactory. Indeed, the very small set of allowable modifications leads to a style shape that differs significantly from the desired i, as corroborated by Fig. 5 and by the cosine between the desired eigenvector and the one obtained that is just 0.865, while the natural frequency is sixty.8 Hz.
Comparing between the desired style and the one obtained with dynamic structural modification alone (cosine between the ii vectors: 0.865)
Since both state-feedback control and dynamic structural modification significantly miss the control specifications when used alone, the use of the proposed hybrid command is a reasonable way to heave the achievement of the desired performances.
Numerical solution
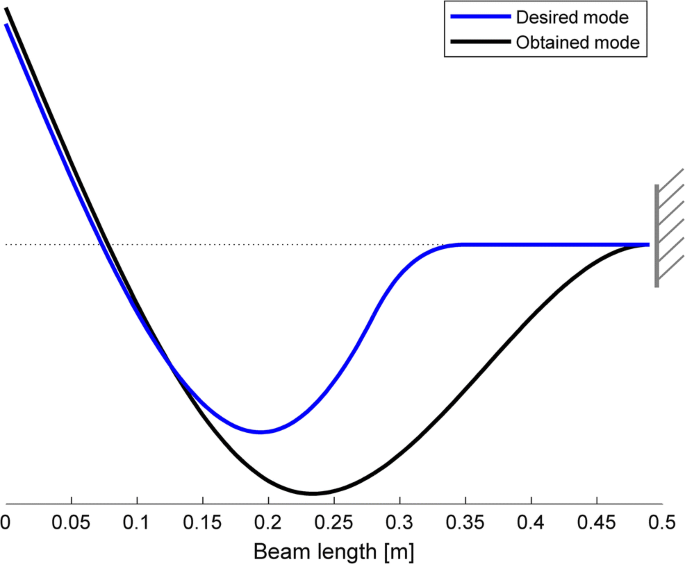
The awarding of dynamic structural modification shapes finer the allowable subspace by means of the two additional lumped masses stated in Tabular array 1. If the bodily land is supposed to be fed back, the airtight-loop pole at 50 Hz can exist exactly obtained, because of controllability, and the projection of the desired eigenvector onto the new commanded subspace provides a significantly ameliorate approximation of the target. The achievable mode shape is nigh parallel to the desired one, every bit depicted in Fig. half-dozen, and the cosine reaches 0.997. The overall comeback can be also inferred from Table 2, which compares the style shapes, the natural frequencies and the cosines in the cases of original organisation, passive modifications lone, active command alone and hybrid control.
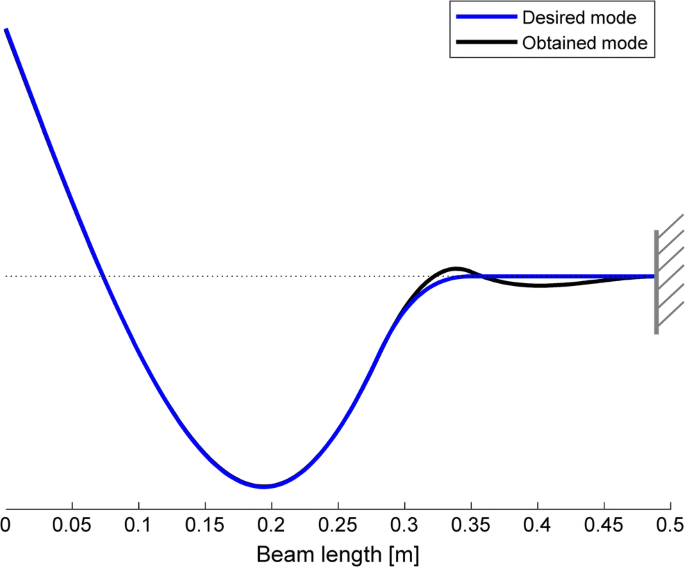
Comparison of the desired mode and the one obtained with hybrid control and nominal value of the system model (cosine between the ii vectors: 0.997)
Experimental implementation of the passive modifications
Two masses made of steel have been manufactured to gauge the optimal masses computed past solving the constrained rank-minimization problem. Since lumped masses do non provide a true representation of the actual construction, information technology has been chosen to include in the model the nodal rotational moment of inertia of the two masses (see Table 1), even if moments of inertia accept not been included among the blueprint variables. Hence, they can be seen as perturbations of the ideal model. Past accounting for the actual features of the mass modifications, the best assignable eigenvector slightly worsens, as shown in Fig. 7, and the cosine with the desired one is 0.995. This value is clearly still very satisfactory, and the comeback compared with the sole agile control is meaningful. A different blueprint of the two masses, east.thousand. with high-density materials, might allow the actual system to better fit the theoretical expectations. Nonetheless, the outcome obtained is accurate enough for the goals of this experimental validation.
Comparison between the desired mode and the i obtained with hybrid control and actual value of the system model (cosine between the ii vectors: 0.995)
Synthesis of the state observer
Given the difficulties in measuring all the 14 variables of the displacement vector, the control strength is computed as
$$ {f}_C=-{\mathbf{Chiliad}}^{\mathrm{T}}\hat{\boldsymbol{q}} $$
(36)
in lieu of the theoretical relation f C = −G T q , where \( \lid{\boldsymbol{q}} \) is the estimated value of the actual displacement vector q . The speed gain F is set to null since it is not wanted to modify the fashion damping.
The two following measurements have been called every bit the sensed output, to ensure adequate observability and hence the beingness of reliable estimates even in the presence of modelling errors and measurement noises:
-
a pair of resistive strain gauges, in a one-half-bridge configuration, to measure the local strain. The strain ε is divers through the shape function of the Euler-Bernoulli beam and is a linear combination of the displacements of the nodes of the finite element where the strain gauges are placed (whose length is denoted as 50), as depicted in Fig. viii:
Fig. 8 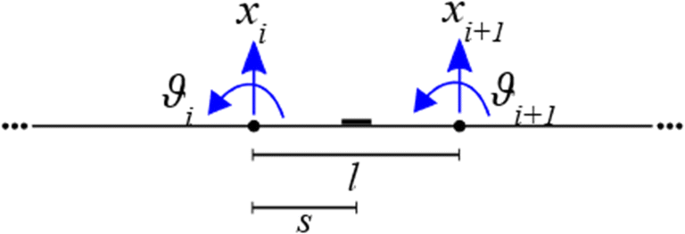
Definition of the sensed strain
$$ \varepsilon =\left\{-\frac{half-dozen}{50^2}+\frac{12s}{l^3}\kern0.5em -\frac{4}{l}+\frac{6s}{l^2}\kern0.5em \frac{6}{l^2}-\frac{12s}{50^3}\kern0.5em -\frac{2}{l}+\frac{6s}{50^2}\right\}\left\{\begin{array}{c}{x}_i\\ {}{\vartheta}_i\\ {}{x}_{i+ane}\\ {}{\vartheta}_{i+1}\end{array}\right\} $$
(37)
The two strain gauges have been placed at 175 mm from the free-end of the beam since this location ensures a good observability and a good signal-to-racket ratio, in particular for the vibrational manner of interest.
-
a laser doppler vibrometer to get direct measurement of the velocity of a point near the free end of the beam, which is the part of the system that vibrates the nearly.
Other sensor configurations could be adopted provided that they ensure adequate organization observability.
In the light of all the critical issues discussed in Section v, an accurate tuning of the state observer has been performed in this experimental campaign both through a wise synthesis of the system model and the tuning of the state observer gain.
Since the beam has negligible outcome on the slip-table, the table dispatch \( {\ddot{x}}_s \) has been assumed as the exogenous input for the model of the state observer, rather than strength f A driving the skid-tabular array (which is also difficult to measure). \( {\ddot{10}}_s \) has been measured through an ICP accelerometer placed on the moving table (encounter Fig. 1). Hence, the country-space model for the observer synthesis, that fits the one in (18) is the following one:
$$ \left\{\begin{array}{c}\ddot{\boldsymbol{q}}\\ {}\dot{\mathbf{q}}\end{assortment}\correct\}=\left[\begin{assortment}{cc}-{\mathbf{Thousand}}^{-i}\mathbf{C}& -{\mathbf{M}}^{-1}\mathbf{Grand}\\ {}\mathbf{I}& \mathbf{0}\end{array}\right]\left\{\begin{array}{c}\dot{\mathbf{q}}\\ {}\boldsymbol{q}\end{array}\right\}+\left\{\begin{array}{c}{\mathbf{M}}^{-1}\mathbf{B}\\ {}\mathbf{0}\terminate{assortment}\right\}{f}_C+\left\{\begin{array}{c}-\mathbf{Southward}\\ {}\mathbf{0}\end{array}\right\}{\ddot{x}}_s $$
(38)
Model reduction has been and then performed by retaining the 2 lowest-frequency vibrational modes (i.e. retaining 4 coordinates in the reduced order model), while discarding the 5 higher frequency ones. A first-order, depression-laissez passer filter with a cut-off frequency at 350 Hz has been also adopted to farther reduce observation spillover.
As for the observer proceeds matrix L (see (24)), it has been computed through the Kalman'south theory every bit follows:
$$ \mathbf{Fifty}=\mathbf{P}{{\mathbf{C}}_R}^T{\mathbf{R}}^{-1} $$
(39)
Matrix P is the solution of the fourth dimension-infinite Riccati'south equation, matrices Q and R are parameters representing the expected measurement and procedure noise covariance matrices:
$$ {{\mathbf{A}}_R}^T\mathbf{P}+\mathbf{P}{\mathbf{A}}_R-\mathbf{P}{{\mathbf{C}}_R}^T{\mathbf{R}}^{-1}{\mathbf{C}}_R\mathbf{P}+\mathbf{Q}=\mathbf{0} $$
(xl)
The sampling time adopted is 1 ms, for trading-off between the needs of high-rate control and estimation, numerical stability and low computational effort, while the numerical integration of the differential equations of the state observer has been done by means of the explicit quaternary order Runge-Kutta scheme.
An example of the effectiveness of the figurer is shown in Fig. nine, which compares the estimated and the bodily values measured by the vibrometer (upper figure) and the strain (lower figure) during a frequency sweep (only an excerpt is shown to provide a clearer representation). The measured and the estimated signals are well-nigh overlapped, and the estimation error is negligible. Additionally, information technology tin can be noticed that the country observer filters measurement dissonance, such equally for instance the fasten recorded in the speed measurement at nigh time i.3 s, thanks to the model used in the prediction phase.
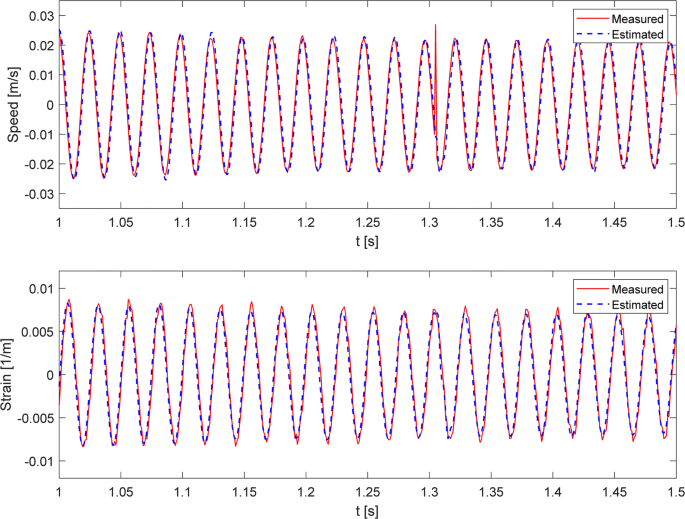
Comparison of actual and estimated quantities
All these choices lead to an expected natural frequency of the desired mode that is 49.ix Hz, as computed through the model in (28). The same model reveals that the cosine betwixt the theoretical expected eigenvector (i.e. the one assuming feedback of the bodily and full state vector, computed through the corrected model that includes moment of inertia of the added masses) and the ane perturbed by the observer (i.e. the one computed through the dynamic matrix in (28)) is higher than 0.9999 for both the existent and the imaginary part. The differences with respect to the target values (i.e. without observer and with the full order model) are conspicuously negligible and therefore the choice of the reduced model has negligible impact on the overall solution. Hence, the proposed methodology is an constructive arroyo for the integrated design and for forecasting the effect of the state observer.
Experimental cess of the eigenstructure assignment
The control gains have been computed through the method proposed by Ram and Mottershead (2007), and subsequently extended in Ouyang (2011) and Ouyang et al. (2013) for disproportionate systems, which provides an effective and reliable solution for the case of rank-ane control. Even so, whatever method could be used.
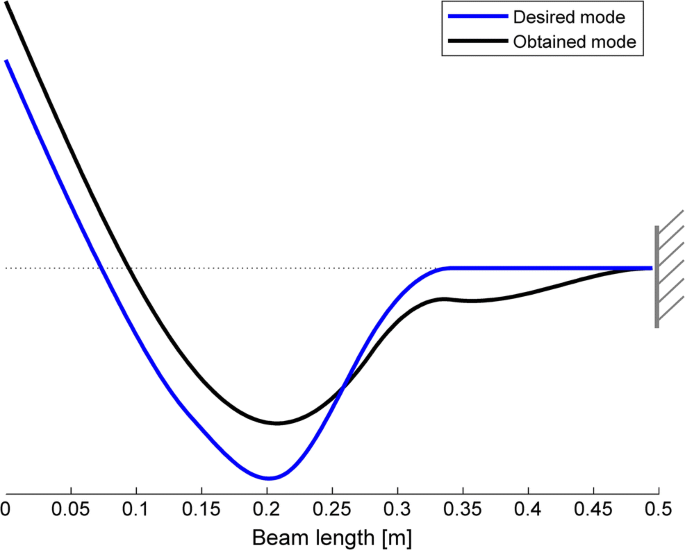
The experimental results obtained bear witness that the control scheme employed succeeded in boosting the achievement of the control specifications. Indeed, the desired mode shape of the closed-loop pole at 50 Hz is very close to the desired i. Figure 10 shows the mode shape identified experimentally (merely the translational components of the eigenvector has been identified, and hence it is represented with a linear interpolation) and compares it with the desired i. The cosine of the angle betwixt the obtained mode and the desired one is 0.966. This is an excellent result that approximates very tightly the theoretical expectations. The divergence is mainly due to the approximation of the lumped masses through two masses with finite moment of inertia (as already discussed and shown in Fig. 7) and to the unavoidable presence of unmodeled and uncertain dynamics (peculiarly because of the piezoelectric actuator and his nonlinearities and divergence from the platonic model). Indeed, the cosine of the bending between the experimental mode and the best achievable eigenvector, i.e. the "numerical with bodily model" depicted through a black line in Fig. 11, is 0.997. This result fits very closely the theoretical expectations since the cosine between the best achievable eigenvector and the ane computed from the augmented model in (28), which included the controlled system and the observer, is 0.999. Hence, just a negligible downgrade of the outcome (i.east. from one to 0.999) is due to the observer because of a wise design of the observer itself, that has allowed reducing spillover. Once more, this result proves that the observer and the reduced model has negligible bear upon on the overall solution, due to a wise synthesis of the observer in accordance with the theory proposed in Section v.1.
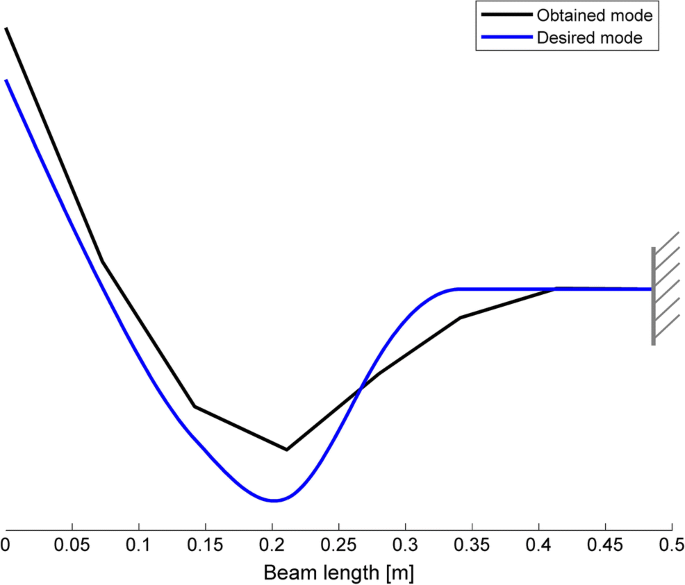
Comparison betwixt the desired mode and the 1 obtained experimentally (cosine betwixt the two vectors: 0.966)
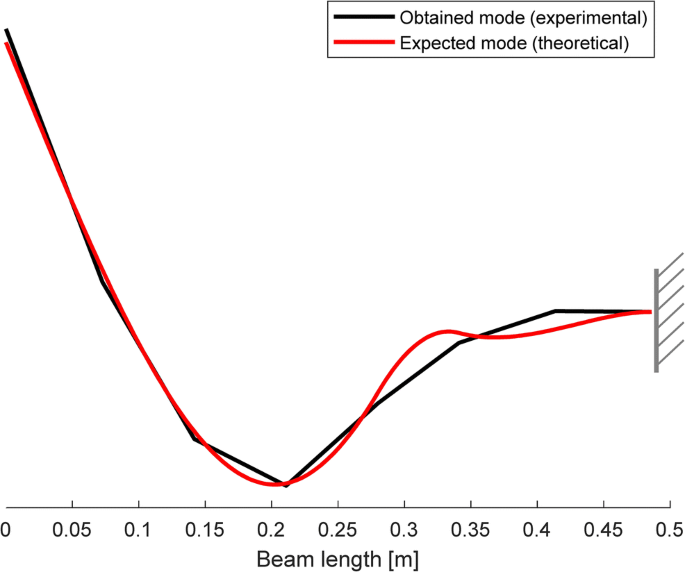
Analysis of the spillover effects with hybrid control: comparison betwixt the theoretical expected eigenvector (with bodily state feedback) and the one obtained experimentally (cosine between the two vectors: 0.997)
Table 3 summarizes the cosine comeback due to the proposed hybrid control, by comparing the chief results of the numerical and experimental investigation. Overall, a great improvement has been obtained, by proving the effectiveness of theory developed and of the comprehensive method proposed, that includes the synthesis of the controller, of the observer and of the physical modifications.
Conclusions
This paper introduced a hybrid method for structural optimization through eigenstructure assignment in an active cantilever axle by exploiting the concurrent design of the physical modifications of the system rubberband and inertial parameters, and the synthesis of the state-feedback controller. The optimal concrete modifications shape the allowable subspace in such a mode that it spans a closer approximation of the desired eigenvector compared with the one achievable by the original system. The method is suitable for underactuated systems, such every bit the studied one, where the size of the prepare of achievable eigenvectors makes EA challenging: the concurrent use of both the techniques overcome the limitations of the utilise of either passive modifications or active command solitary, by enlarging the set of assignable eigenpairs.
The optimal solution is computed by solving a rank-minimization problem with constraints on the design variables, that arises from the definition of the allowable subspace. A convex optimization problem is formulated through the semidefinite embedding lemma and the so-called trace heuristics, and reliable numerical solution can be performed.
The paper covers all the problems for the implementation of this control approach in a real system, including the synthesis of a state observer for replacing the actual state with the estimated 1. The use of a reduced-order observer, to let for real fourth dimension computation, causes spillover of the closed-loop poles and perturbation of the mode shapes that might severely downgrade the achievable performances. A model to cope with this event is therefore presented and the coupling with the controller is shown.
The experimental results obtained are very satisfactory. First of all, the proposed method succeeded in achieving a tight approximation of the desired performances both in terms of mode shape and natural frequency: the cosine between the desired way shape and the achieved one is 0.966, while active command solitary leads to 0.524. Secondly, the theoretical expectations closely fit the experimental results, thanks to a careful design of the state observer introducing negligible perturbation of the desired eigenpair: the perturbation due to the observer is small and the cosine between the expected eigenvector and the one obtained in the testbed is 0.997.
References
-
Andry AN, Shapiro EY, Chung JC (1983) Eigenstructure assignment for linear systems. IEEE Trans Aerosp Electron Syst 5:711–729
-
Araújo JM, Dórea CE, Gonçalves LM, Datta BN (2016) State derivative feedback in 2d-lodge linear systems: a comparative assay of perturbed eigenvalues under coefficient variation. Mech Syst Signal Process 76:33–46
-
Aydin E, Dutkiewicz M, Öztürk B, Sonmez Chiliad (2020). Optimization of rubberband spring supports for cantilever beams. Struct Multidiscip Optim 62:55–81. https://doi.org/10.1007/s00158-019-02469-iii
-
Belotti R, Richiedei D (2018) Dynamic structural modification of vibrating systems oriented to eigenstructure assignment through agile command: a concurrent approach. J Sound Vib 422:358–372
-
Belotti R, Richiedei D, Trevisani A (2016) Optimal design of vibrating systems through partial eigenstructure assignment. J Mech Des 138(seven):071402 (8 pages)
-
Belotti R, Richiedei D, Trevisani A (2017) Concurrent design of active command and structural modifications for eigenstructure assignment on a cantilever beam. In ASME 2017 International design engineering science technical conferences and computers and information in engineering science briefing. American Society of Mechanical Engineers Digital Collection
-
Belotti R, Caracciolo R, Palomba I, Richiedei D, Trevisani A (2018a) An updating method for finite element models of flexible-link mechanisms based on an equivalent rigid-link system. Daze Vib 2018:1–xiv. https://doi.org/ten.1155/2018/1797506
-
Belotti R, Ouyang H, Richiedei D (2018b) A new method of passive modifications for partial frequency assignment of general structures. Mech Syst Signal Process 99:586–599
-
Belotti R, Richiedei D, Tamellin I (2020) Antiresonance assignment in bespeak and cross receptances for undamped vibrating systems. J Mech Des 142(2):022301 (7 pages. https://doi.org/10.1115/1.4044329
-
Caracciolo R, Richiedei D, Trevisani A (2008) Robust piecewise-linear land observers for flexible link mechanisms. J Dyn Syst Meas Control 130(3). https://doi.org/10.1115/1.2909600
-
Corr LR, Clark WW (2002) Active and passive vibration confinement using piezoelectric transducers and dynamic vibration absorbers. J Mech Behav Mater 13(2):117–134
-
Delissen A, van Keulen F, Langelaar M (2020) Efficient limitation of resonant peaks by topology optimization including modal truncation augmentation. Struct Multidiscip Optim 61:2557–2575. https://doi.org/ten.1007/s00158-019-02471-9
-
Fazel Yard, Hindi H, Boyd SP (2001) A rank minimization heuristic with application to minimum society system approximation. In Proceedings of the 2001 American Control Conference six:4734–4739
-
Fazel M, Hindi H, Boyd SP (2003) Log-det heuristic for matrix rank minimization with applications to Hankel and Euclidean distance matrices. In Proceedings of the 2003 American Command Conference iii:2156–2162
-
Franklin GF, Powell JD, Emami-Naeini A, Sanjay HS (2015) Feedback command of dynamic systems. Pearson, London
-
Gaudenzi P, Carbonaro R, Benzi E (2000) Control of beam vibrations by means of piezoelectric devices: theory and experiments. Compos Struct 50(four):373–379
-
Hauser BR, Wang BP (2018) Optimal design of a parallel beam organisation with elastic supports to minimize flexural response to harmonic loading using a combined optimization algorithm. Struct Multidiscip Optim 58(four):1453–1465
-
Hehenberger P, Follmer One thousand, Geirhofer R, Zeman Thou (2013) Model-based system blueprint of annealing simulators. Mechatronics 23(3):247–256
-
Hernandes JA, Suleman A (2014) Structural synthesis for prescribed target natural frequencies and mode shapes. Shock Vib, Article ID 173786 2014 https://doi.org/10.1155/2014/173786
-
Jihong Z, Weihong Z (2006) Maximization of structural natural frequency with optimal support layout. Struct Multidiscip Optim 31(six):462–469
-
Kim Y, Kim HS, Junkins JL (1999) Eigenstructure assignment algorithm for mechanical second-order systems. J Guid Control Dyn 22(5):729–731
-
Lee J (2019) Multi-objective optimization example report with agile and passive blueprint in building engineering. Struct Multidiscip Optim 59(ii):507–519
-
Moore B (1976) On the flexibility offered by state feedback in multivariable systems across airtight loop eigenvalue assignment. IEEE Trans Autom Control 21(5):689–692
-
Ouyang H (2011) A hybrid control approach for pole assignment to second-order asymmetric systems. Mech Syst Signal Process 25(1):123–132
-
Ouyang H, Richiedei D, Trevisaniv AV (2013) Pole assignment for control of flexible link mechanisms. J Sound Vib 332(2013):2884–2899
-
Palomba I, Richiedei D, Trevisani A (2015) Energy-based optimal ranking of the interior modes for reduced-gild models nether periodic excitation. Shock Vib 2015:1–10. https://doi.org/10.1155/2015/348106
-
Palomba I, Richiedei D, Trevisani A (2017) Kinematic country interpretation for rigid-link multibody systems by ways of nonlinear constraint equations. Multibody Syst Dyn twoscore(1):1–22
-
Preumont A (2011) Vibration control of agile structures, an introduction, 3rd edn. Springer International Publishing, Cham. https://doi.org/10.1007/978-94-007-2033-half-dozen
-
Ram YM, Mottershead JE (2007) Receptance method in active vibration command. AIAA J 45(3):562–567
-
Richiedei D, Trevisani A (2017) Simultaneous agile and passive control for eigenstructure assignment in lightly damped systems. Mech Syst Bespeak Process 85:556–566
-
Richiedei D, Tamellin I, Trevisani A (2019) A general approach for antiresonance consignment in undamped vibrating systems exploiting auxiliary systems. In: Uhl T (ed) Advances in mechanism and machine science. IFToMM WC 2019. Mechanisms and machine scientific discipline, vol 73. Springer, Cham, pp 4085–4094. https://doi.org/10.1007/978-iii-030-20131-9_407
-
Richiedei D, Tamellin I, Trevisani A (2020) Simultaneous assignment of resonances and antiresonances in vibrating systems through changed dynamic structural modification. J Sound Vib 485, 27 Oct 2020, 115552:xix. https://doi.org/10.1016/j.jsv.2020.115552
-
Sanjurjo Due east, Dopico D, Luaces A, Naya MÁ (2018) State and force observers based on multibody models and the indirect Kalman filter. Mech Syst Signal Process 106:210–228
-
Schulz MJ, Inman DJ (1994) Eigenstructure assignment and controller optimization for mechanical systems. IEEE Trans Control Syst Technol 2(2):88–100
-
Tang J, Wang KW (2004) Vibration confinement via optimal eigenvector assignment and piezoelectric networks. J Vib Acoust 126(ane):27–36
-
Thomas Due south, Li Q, Steven Thousand (2020) Topology optimization for periodic multi-component structures with stiffness and frequency criteria. Struct Multidiscip Optim 61:2271–2289. https://doi.org/10.1007/s00158-019-02481-7
-
Triller MJ, Kammer DC (1997) Improved eigenstructure assignment controller design using a substructure-based coordinate arrangement. J Guid Control Dyn 20(five):941–948
-
Xiao Thousand, Lu D, Breitkopf P, Raghavan B, Dutta Due south, Zhang W (2020) On-the-fly model reduction for large-calibration structural topology optimization using principal components analysis. Struct Multidiscip Optim 62:209–230. https://doi.org/10.1007/s00158-019-02485-3
-
Yan 1000, Wang BP (2020) Two new indices for structural optimization of complimentary vibration suppression. Struct Multidiscip Optim 61:2057–2075. https://doi.org/10.1007/s00158-019-02451-z
-
Zhai J, Zhao 1000, Shang L (2017) Integrated pattern optimization of structural size and control system of piezoelectric curved shells with respect to sound radiations. Struct Multidiscip Optim 56(six):1287–1304
-
Zhang J, Ouyang H, Yang J (2014) Partial eigenstructure consignment for undamped vibration systems using acceleration and displacement feedback. J Sound Vib 333(1):one–12
-
Zheng S, Zhao 10, Yu Y, Sunday Y (2017) The gauge reanalysis method for topology optimization under harmonic force excitations with multiple frequencies. Struct Multidiscip Optim 56(5):1185–1196
Acknowledgments
Open access funding provided by Università degli Studi di Padova within the CRUI-CARE Agreement.
Author information
Affiliations
Corresponding author
Ethics declarations
Conflict of involvement
The authors declare that they have no disharmonize of interest.
Replication of the results
The Appendix proposes the Matlab lawmaking for the computation of the optimal structural modifications for hybrid control, past implementing the rank-minimization method in (16). It requires the toolbox YALMIP (https://yalmip.github.io). The data for replicating the test can be obtained from the description of the test rig provided in Section 6.
Additional information
Publisher's notation
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Responsible Editor: Somanath Nagendra
Appendix
Appendix

Rights and permissions
Open Admission This article is licensed under a Creative Commons Attribution 4.0 International License, which permits employ, sharing, adaptation, distribution and reproduction in any medium or format, as long as y'all requite appropriate credit to the original author(s) and the source, provide a link to the Artistic Commons licence, and indicate if changes were fabricated. The images or other tertiary party material in this article are included in the article'south Creative Commons licence, unless indicated otherwise in a credit line to the fabric. If cloth is non included in the article'southward Creative Eatables licence and your intended use is not permitted by statutory regulation or exceeds the permitted utilise, yous will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Reprints and Permissions
Most this article
Cite this article
Belotti, R., Richiedei, D. & Trevisani, A. Multi-domain optimization of the eigenstructure of controlled underactuated vibrating systems. Struct Multidisc Optim 63, 499–514 (2021). https://doi.org/10.1007/s00158-020-02709-x
-
Received:
-
Revised:
-
Accustomed:
-
Published:
-
Issue Appointment:
-
DOI : https://doi.org/10.1007/s00158-020-02709-x
Keywords
- Optimal blueprint
- Eigenstructure assignment
- Structural modification
- Active control
- Rank minimization
Source: https://link.springer.com/article/10.1007/s00158-020-02709-x
0 Response to "Solve for the Exact Same Eigenvalues Again Using an Optimization Approach"
Post a Comment